傅里叶变换的基本性质: 可分离性,平移性, 周期性, 共轭对称性,旋转不变性,比例性,平均值,卷积定理

可分离性

可以将 二维傅里叶变换 转换为 两次 一维傅里叶变换.

正变换:

$$F(u,v)=\frac 1N \sum \limits_{x=0}^{N-1}e^{-j2\pi ux/N} \sum \limits_{y=0}^{N-1}f(x,y)e^{-j2\pi vy/N}$$

$$u,v=0,1,\ldots,N-1$$

反变换:

$$f(x,y)=\frac 1N \sum \limits_{u=0}^{N-1}e^{j2\pi ux/N} \sum \limits_{v=0}^{N-1}F(u,v)e^{j2\pi vy/N}$$

$$x,y=0,1,\ldots,N-1$$

平移性

傅里叶变换的平移性是指，将$f(x,y)$ 乘以一个指数项，相当于把$F(u,v)$其二维离散傅里叶变换的频域中心移动到新的位置。

$$f(x,y)e^{j2\pi (u_0x+v_0y)/N} \Leftrightarrow F(u-u_0,v-v_0)$$

$$f(x-x_0,y-y_0) \Leftrightarrow F(u,v)e^{-j2\pi (ux_0+vy_0)/N}$$

将图像频谱的原点从起始点（0,0）移到图像的中心点，只需令$u_0=v_0=N/2$

此时有:

$$e^{j2\pi (u_0x+v_0y)/N} = e^{j\pi (x+y)} = (-1)^{x+y}$$

$$f(x,y)(-1)^{x+y}\Leftrightarrow F\left(u - \frac N2,v-\frac N2\right)$$

即为"零点漂移"

周期性

傅里叶变换和反变换均以N为周期，即:

$$F(u,v)=F(u+N,v)=F(u,v+N)=F(u+N,v+N)$$

傅里叶变换的周期性表明，尽管$F(u,v)​$有无穷多个u和v的值,但只需根据在任意周期内的N个值就可以 从$F(u,v)​$得到$f(x,y)​$ 。只需一个周期内的变换就可以将完全确 定。这一性质对于 在空域里也同样成立.

共轭对称性

如果是实函数，则它的傅里叶变换具有共轭对称性：

$$F(u,v)=F^*(-u,-v)$$

其中,$F^*(u,v)$是$$F(u,v)$$的复共轭。

图像傅里叶变化的周期性和共轭对称性便于图像的频谱分析和显示。

旋转不变性

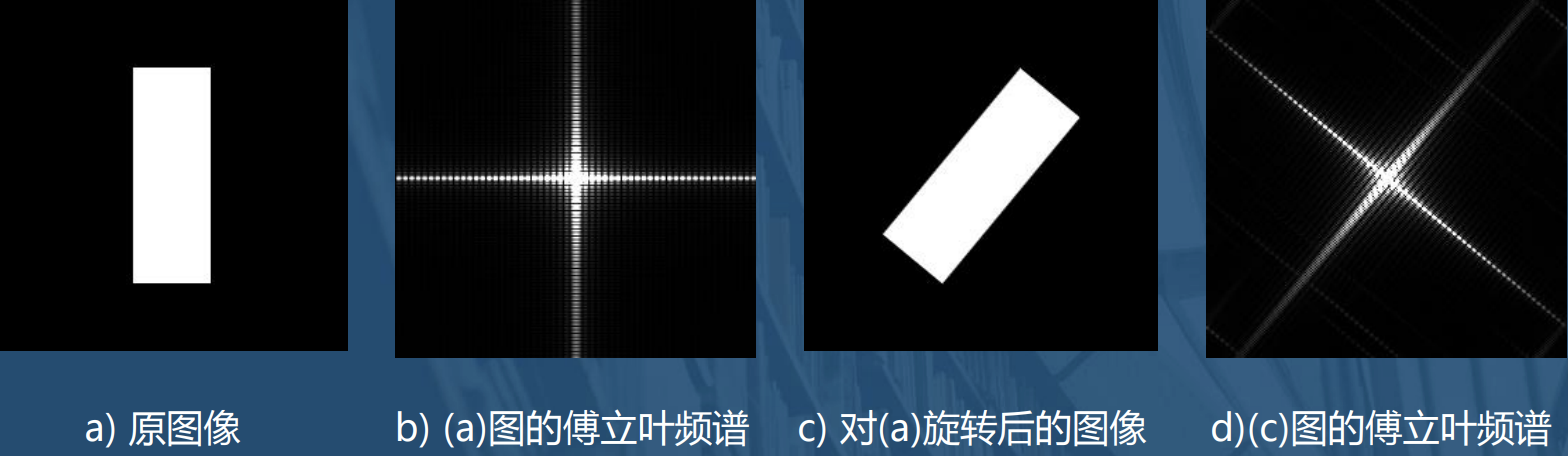
比例性

$$af(x,y)\Leftrightarrow aF(u,v)$$

平均值

$$\bar f(x,y)=\frac 1{MN} \sum\limits_{x=0}^{M-1}\sum\limits_{y=0}^{N-1}(x,y)$$

$$F(0,0)=\frac 1{MN}\sum \limits_{x=0}^{M-1}\sum\limits_{y=0}^{N-1}f(x,y)$$

所以:

$$\bar f(x,y)=F(0,0)$$

卷积定理

$$f(x)*g(x)\Leftrightarrow F(u)G(u)$$

$$f(x)g(x)\Leftrightarrow F(u)*G(u)$$

二维亦如此.

空间卷积的DFT是频率域中相应变换的乘积，反之也成立。

卷积定理在滤波技术中有着非常重要的应用。