频域图像处理基本步骤

空间域：（spatial domain）也叫空域，即所说的像素域，在空域的处理就是在像素级的处理，如在像素级的图像叠加。通过傅立叶变换后，得到的是图像的频谱。表示图像的能量梯度。

频率域：（frequency domain。）任何一个波形都可以分解用多个正弦波之和。每个正弦波都有自己的频率和振幅。所以任意一个波形信号有自己的频率和振幅的集合。频率域说的就是这个。频率域就是空间域经过傅立叶变换的信号。

频域（频率域）—--—自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。频谱图描述了信号的频率结构及频率与该频率信号幅度的关系。

时域（时间域）—--—自变量是时间,即横轴是时间,纵轴是信号的变化。其动态信号x（t）是描述信号在不同时刻取值的函数。

傅里叶变换是实现从空域或时域到频域的转换工具。

当某些问题在空域里难以解决时,我们就可以通过频域进行解决,然后反变换回空域

基本步骤:

傅里叶级数和傅里叶变换

• 满足一定的数学条件，任何周期函数都可以表示为不同频率的正弦和的形式。

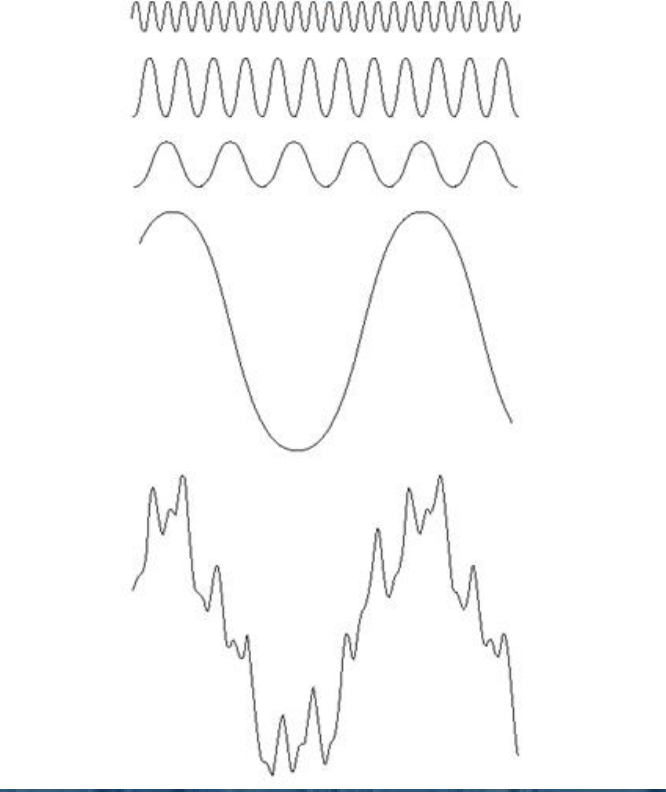
• 满足一定的数学条件，非周期函数也可表示为正弦乘以加权函数积分的形式，即傅里叶变换。
• 用傅里叶级数或傅里叶变换表示的函数特征完全可以通过傅里叶反变换重建，且不会丢失任何信息。 一维离散傅里叶

一维离散傅里叶变换

一维离散傅里叶变换:

$$F(u)=\sum \limits_{x=0}^{N-1} f(x)e^{\frac {-j2\pi ux} N}$$

$$u = 0,1,2 \ldots,N-1$$

反变换:

$$f(x)=\frac 1N \sum \limits_{u=0}^{N-1}F(u)e^{\frac {j2\pi ux}{N}}$$

$$x = 0,1,2 \ldots,N-1$$

二维离散傅里叶变换

二维离散傅里叶变换:

$$F(u,v)=\sum ^{m-1} \limits_{x=0}\sum ^{N-1}\limits_{y=0}f( x,y) e^{-j2\pi \left( \dfrac {ux}{M}+\dfrac {vy}{N}\right) }$$

$$u = 0,1,2 \ldots,M-1$$

$$v = 0,1,2 \ldots,N-1$$

反变换:

$$f(x,y)=\frac 1{MN} \sum ^{m-1} \limits_{u=0}\sum ^{v-1}\limits_{y=0}F(u,v) e^{j2\pi \left( \dfrac {ux}{M}+\dfrac {vy}{N}\right) }$$

$$x = 0,1,2 \ldots,M-1$$

$$y = 0,1,2 \ldots,N-1$$

频谱与相位角

$$F\left( u,v\right) =\left| F\left( u,v \right) \right| e^{j\varphi \left( u,v\right) }=R\left( u,v\right) +jI\left( u,v\right)$$

其中:

$\left|F\left(u,v\right)\right| = \sqrt{R^2\left(u,v\right)+I^2\left(u,v\right)} \tag{幅值}$

$\varphi \left( u,v\right) =\arctan \dfrac {I\left( u,v\right) }{R\left( u,v\right) } \tag{相位角}$

频率成分分布

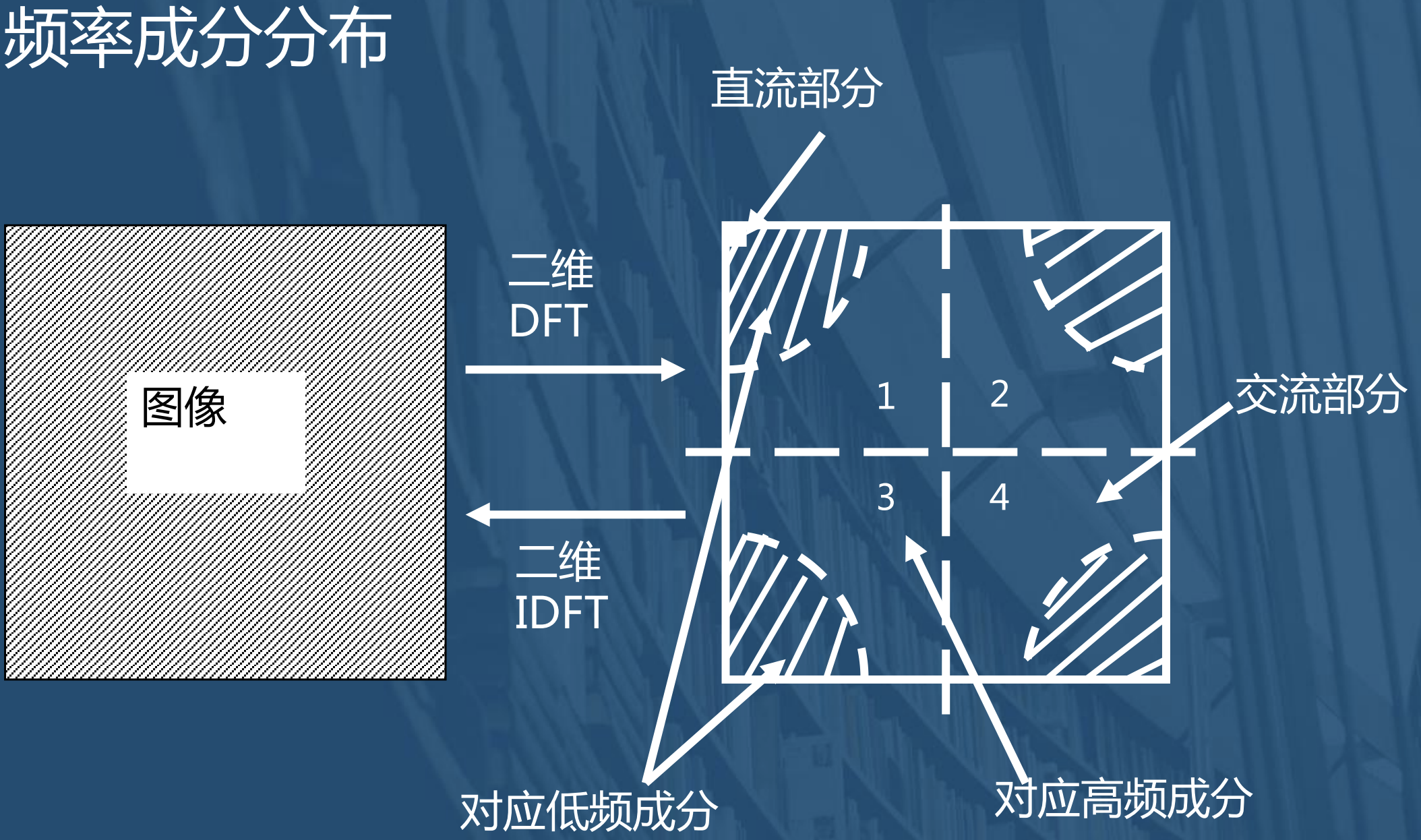
零点漂移

将四角移到中心,即低频成分在中间,高频成分在四周.

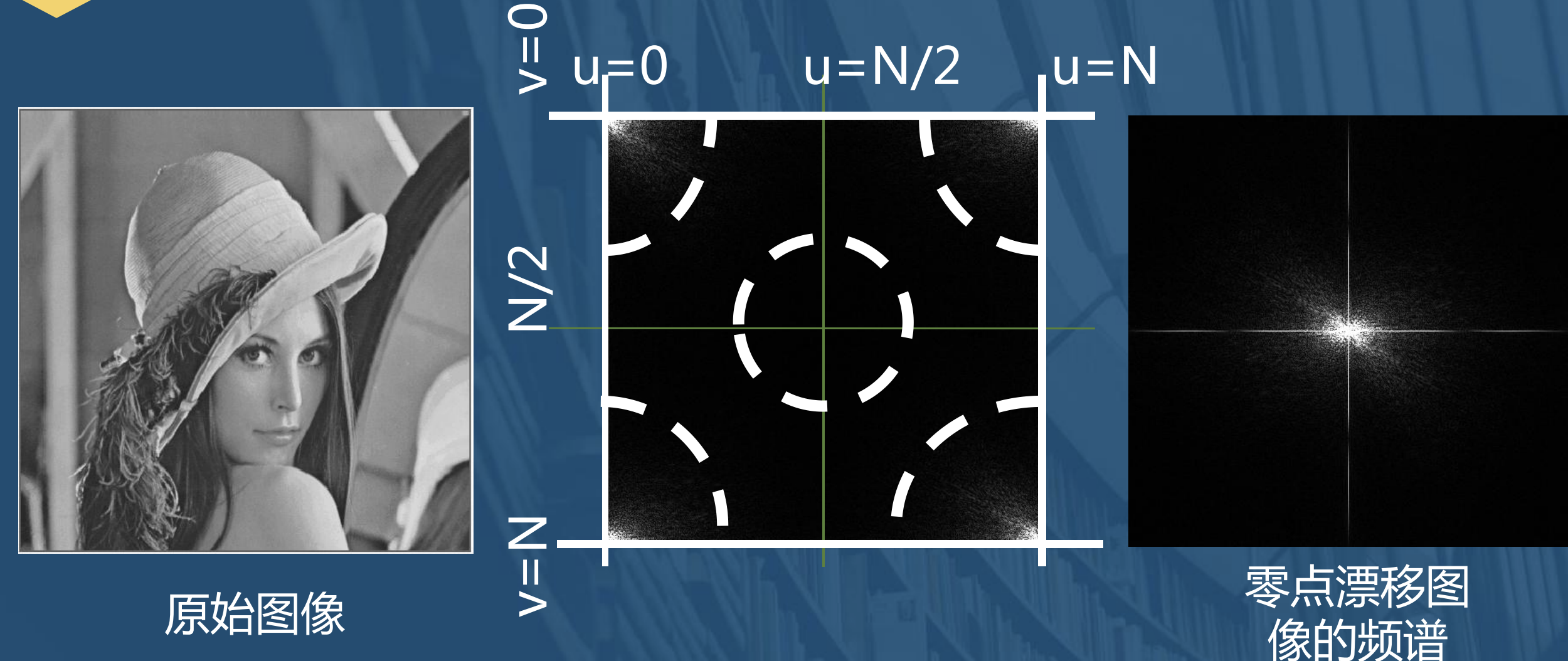
一般傅里叶变换以后一般都会进行零点漂移.

相位谱具有更重要的应用,其记录了像素的位置

所以一般滤波是对幅值谱进行的.