基本概念

几何变换又称橡皮膜变换,就像在一块 橡皮膜上印刷一幅图像，然后根据预定的一组规则拉伸该橡皮膜。

几何变换改变了图像中像素间的空间关系。 由两个基本操作组成:坐标的空间变换（坐标变换）和变换后坐标像素的灰度值（灰度插值）。

坐标变换

坐标变换函数通常用 $T\{\}$ 表示

例如

$$(x'+y')=T\{(x,y)\}=(\frac x 2,\frac y2)$$

表示在两个方向上把原图像缩小一半。

仿射变换

图像处理中常用的坐标变换是仿射变换。

一般形式如下:

$$\left[ \begin{matrix} x' & y' & 1 \end{matrix} \right] = \left[ \begin{matrix} x & y & 1 \end{matrix} \right]T=\left[ \begin{matrix} x&y&1\end{matrix} \right]\left[ \begin{matrix} t_{11}&t_{12}&0 \\\ t_{21} & t_{22} & 0 \\\ t_{31} &t_{32} &1\end{matrix} \right]$$

根据变换矩阵T 中的参数取值不同，实现尺度/旋转/平移等坐标变换

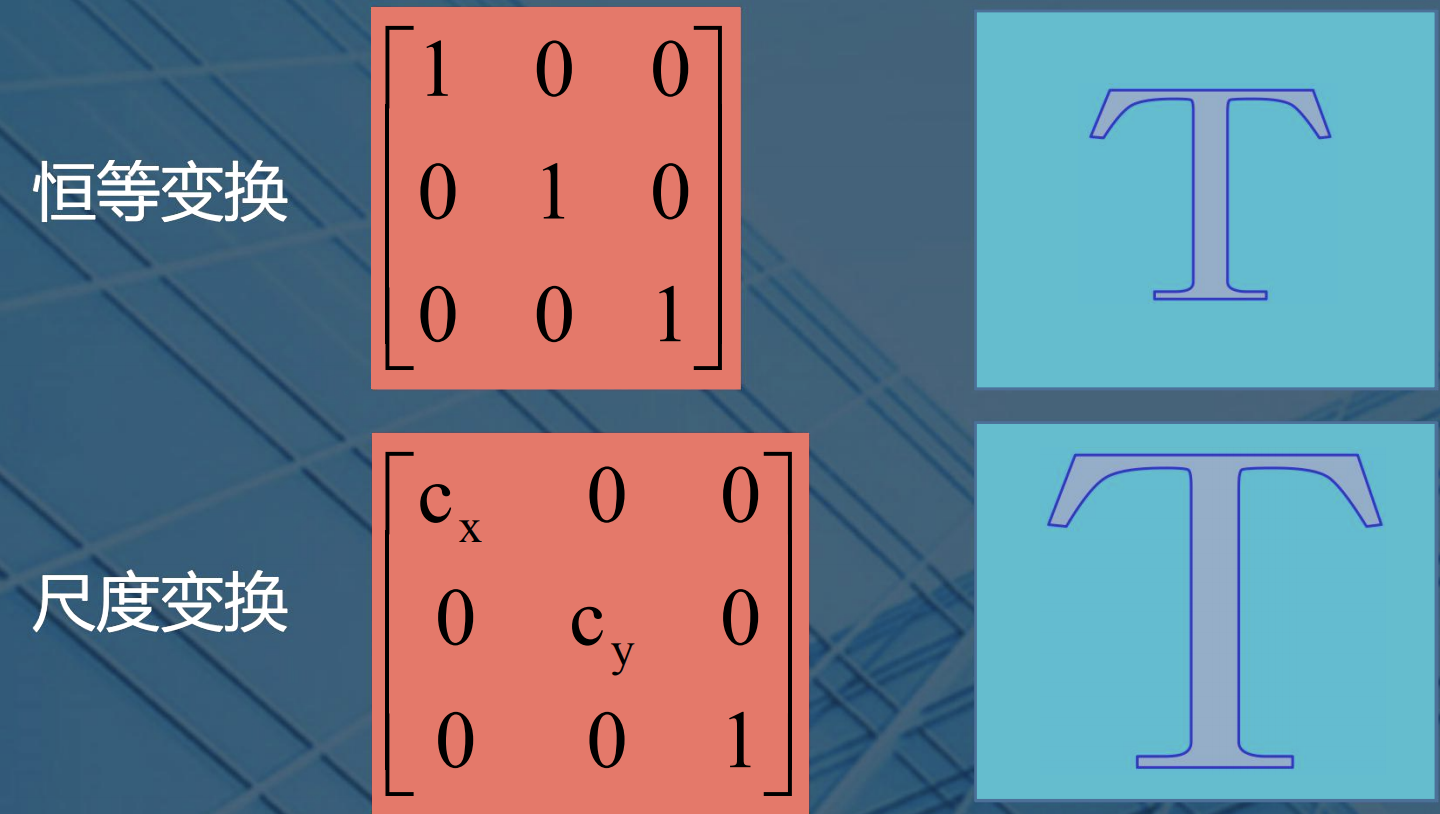
• 恒等变换

$x'=x$

$y'=y$

恒等变换即为原图

• 平移变换

$x'=C_{x}x$

$y'=C_{y}y$

放大与缩小

• 旋转变换

$x'=x\cdot cos( \theta)+y \cdot sin( \theta)$

$y'=x\cdot(-sin( \theta))+y\cdot cos(\theta)$

顺时针旋转$\theta$角度

• 平移变换

$x'=x+t_{x}$

$y'=y+t_{y}$

前向映射和后向映射

• 前向映射:

$$(x',y')=T\{(x,y\}$$

• 后向映射:

$$(x,y)=T^{-1}\{(x',y'\}$$

前向映射中的问题

1. 浮点数坐标

对于数字图像而言，像素坐标是用离散型的非负正 数表示的，但是通过映射函数变换后可能产生浮点数的坐标。

可以用插值算法来处理在几何变换中 出现的浮点坐标像素，它可以通过一系列算法获得 浮点坐标像素的近似值。。

1. 映射不完全

指输入图像的像素总数小于输出图像的像素总数， 这会使得输出图像的部分像素与原始图像没有映射 关系。

例如:

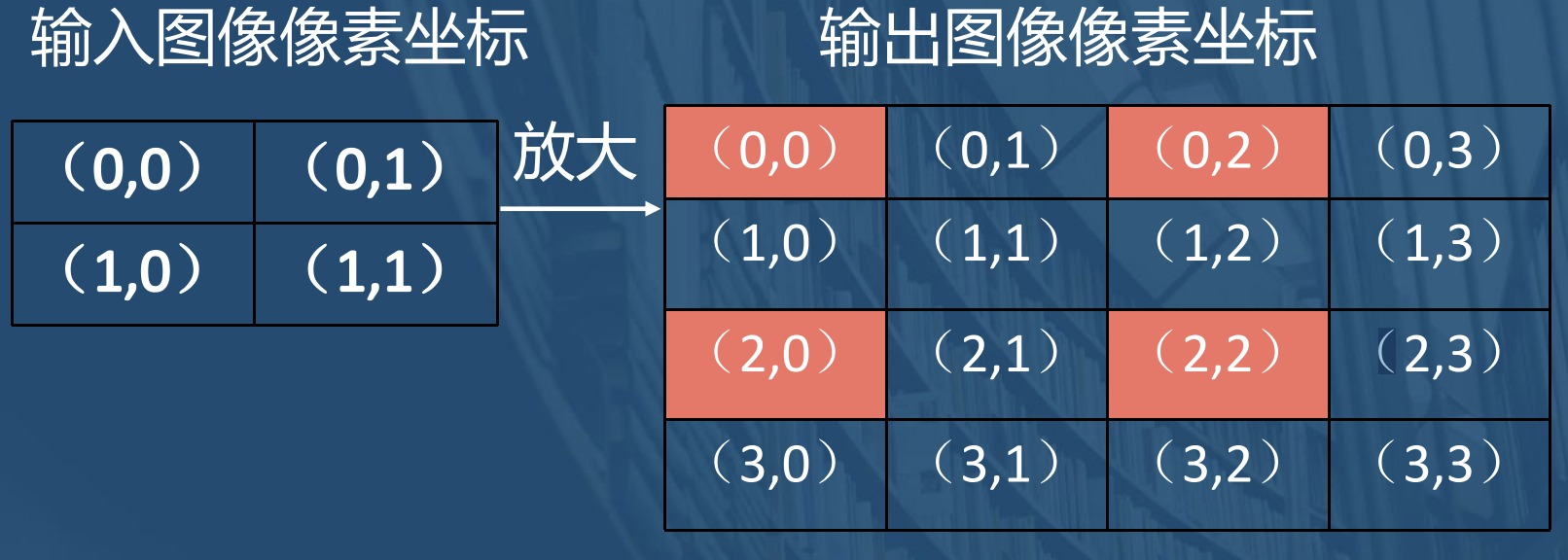
1. 映射重叠

好几个像素点映射变换,取整以后,在同一个像素点上

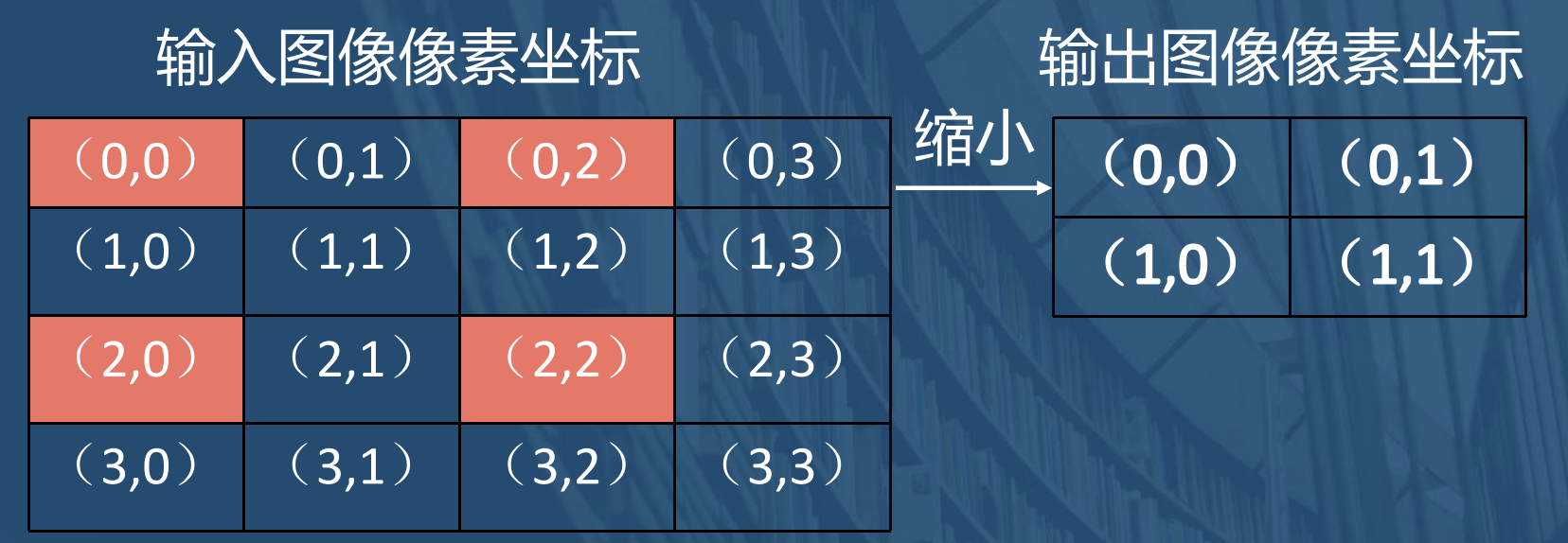
输出图像的每个像素都能通过映射找到输入图像对 应的位置，而不会产生映射不完全和映射重叠的现象。在实际处理中，基本是运用向后映射来进行图像的几何变换的.

后向映射中通过$T^{-1}$进行矩阵反变换后若有小数,可用灰度差值进行处理.