基本关系

一幅图像 $f (x , y)$ 由基本单元像素组成，像素间存在着一定的联系，包括像素的邻域，邻接 和连通，以及像素间的距离。一般地，当指定某个特定的像素时用小写字母（如 p）表示。

邻域

在一幅图像$f(x, y)$中，一个坐标为$ (x , y)$的像 素p的邻近像素组成了该像素的邻域。根据邻近像素的不同定义，可以得到不同的邻域：

• 4-邻域 ( $N_{4} (p)$ )

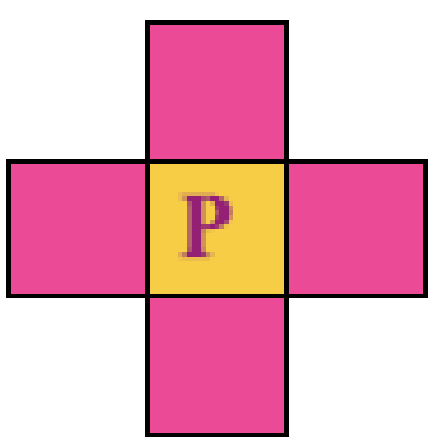
• 8-邻域 ( $N_{8}(p)$ )

• 对角邻域 ( $N_{D}(p)$ )

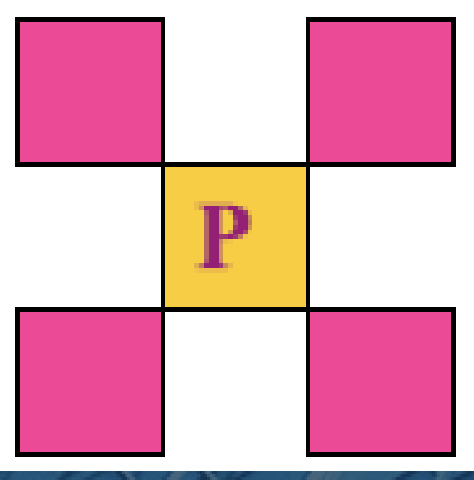
邻接

对于任意两个像素，若一个像素在另一个像素 的邻域中，且它们的灰度值满足特定的相似准则(例如属于某一个灰度值集合)，则称这两个像素是邻接的，有3种像素的邻接：

• 4-邻接

  • 如果q在N4(p)中，满足灰度值条件为集合V 的两个像素p和q是4邻接的。
  • 例：V={1}，且p、q的灰度值都为1.

  | 0 | 0 | 0 |
  | 0 | p | q |
  | 0 | 0 | 1 |

• 8-邻接

  • 如果q在N8(p)中，满足灰度值条件为集合V 的两个像素p和q是8邻接的。
  • 例：V={1}，且p、q的灰度值都为1.

  | 0 | 1 | 0 |
  | 0 | p | 0 |
  | 0 | 0 | q |

• m-邻接

  • 灰度值满足集合V的像素 p和q，若符合下列 两个条件之一：

    • a、q在p的4邻域中；
    • b、q在p的对角领域中，并且q的4邻域与p的 4领域交集像素中没有灰度值属于V。则称p , q两点是m邻接。

连通

设$p(x,y)$与$q(s,t)$之间存在的一条通路，由像素序列组成 ：

$$[(x_{0},y_{0}),(x_{1},y_{1}), ... ,(x_{n},y_{n}),]$$

其中$(x_{i},y_{i})$与$(x_{i-1},y_{i-1}) $ $(1\le i\le n)$相邻接.

$n$ 称为通路的长度,根据邻接类型，分为：

• 4-通路
• 8-通 路
• m-通路。

若像素p和q存在一条通路，则称p和q是连通的，根据通路类型，分为

• 4-连通
• 8-连通
• m-连通。

距离

对于象素p(x,y)、q(s,t)和r(u,v),当:

1. $D(p,q) \ge 0$ (当切仅当$p=q$时等号成立)
2. $D(p,q)=D(q,p)$
3. $D(p,r) \le D(p,q) + D(q,r)$

则称函数D为距离或度量函数

常见的距离函数D有:

• 欧式距离

$$D_{e}(p,q)=[(x-s)^{2}+(y-t)^{2}]^{\frac{1}{2}}$$

距离p的欧式距离小于或等于某一值R的像素都包含在以 p 为圆心且半径为R的圆内。

• 城区距离

$$D_{4}(p,q)=|x-s|+|y-t|$$

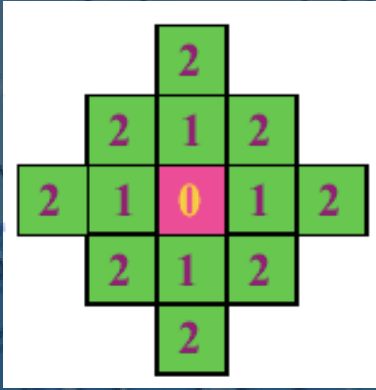
• 棋盘距离

$$D_{8}(p,q)=max(|x-s|,|y-t|)$$

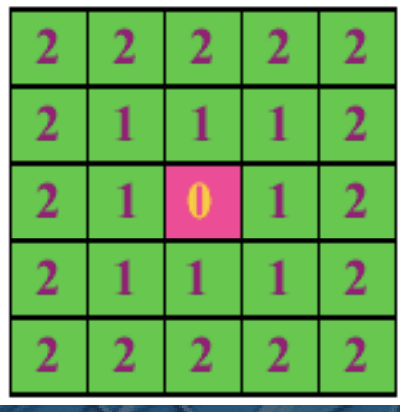
欧式距离给出的结果比较准确，但计算时要进行平方和开方运算，计算量大。 城区距离和棋盘距离均为非欧式距离， 计算量小，但有一定的误差